An example game loop

Suppose Diego, Ruben and Tanja are playing a game of Kwartet. Like John Snow, Diego knows nothing, starting the game by asking a random card to a random player. In this case he asked Tanja for the 'smelly goat' card from the 'farm animals' group. Even before Tanja gives an answer, the knowledge of the players changes. To see what happens with the knowledge we go through the first questions of this game step by step.

Diego: “Tanja, do you have from ‘farm animals’ the ‘smelly goat’?”

Based on this announcement it is common knowledge that Diego has a card of the group ‘farm animals’, otherwise he would not be allowed to ask this question. Moreover, it is common knowledge that he does not have the ‘smelly goat’ card.

Tanja: “No.”

From this point it is common knowledge that Tanja does not have the ‘smelly goat’ card, so everyone now removes the possiblity in their model that Tanja has a ‘smelly goat’ card.

Diego’s turn is over, it is Tanja's turn.

Tanja: “Diego, do you have from ‘farm animals’ the ‘crazy pig’?”

This time again it becomes common knowledge that Tanja has a card of the ‘farm animals’, but she does not have the ‘crazy pig’.

Diego: “Yes.”

Diego gives the ‘crazy pig’ card to Tanja.

Now it is common knowledge that Tanja has the ‘crazy pig’.
It is common knowledge Diego & Ruben do not have the ‘crazy pig’.
Moreover, Ruben and Tanja no longer know whether Diego has a ‘farm animals’ card.

Architecture

To model the structure of a Kripke model, we use python dictionaries. Keys in the dictionaries are representative of propositional atoms in each world, with exception of the agent key which defines the agent relation. Keys are nested; by following the structure the keys are added to define the values of the propositional atoms of a world. The final value is an Operator of the K language, [M,K,not]; here not can be seen as removed from the model. A visualisation of the structure can be found in Figure 1. The reasoning behind the key ordering in our data structure is that, a possible group is know by an agent before a single card is known. Furthermore a card group is of higher order than a card, optimizing the search for possible options. If a card is known, the group is known, so there is no option of a known card in a M or deleted group.

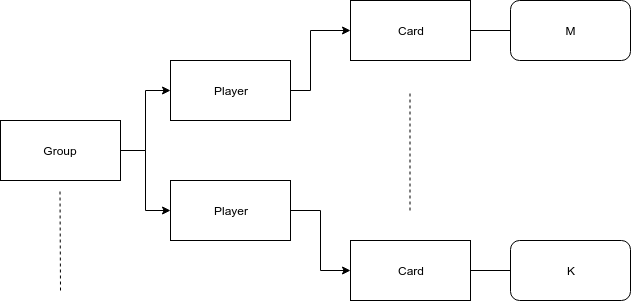
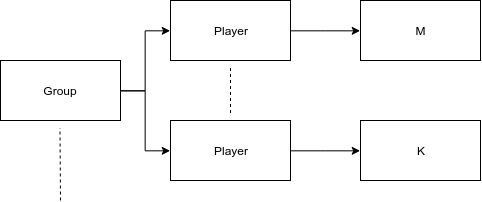
While playing different strategies we require to look at different observables, as an example we need to look not only at cards but also at card groups (Figure 2).In our model we require a seperate model for each of these observables, this is because of a limitation in our datastructure. We cannot "remove" a world in the model without affecting worlds that should still be accesble from other worlds. As an example we cannot remove a group for one agent without removing the group for all agents.

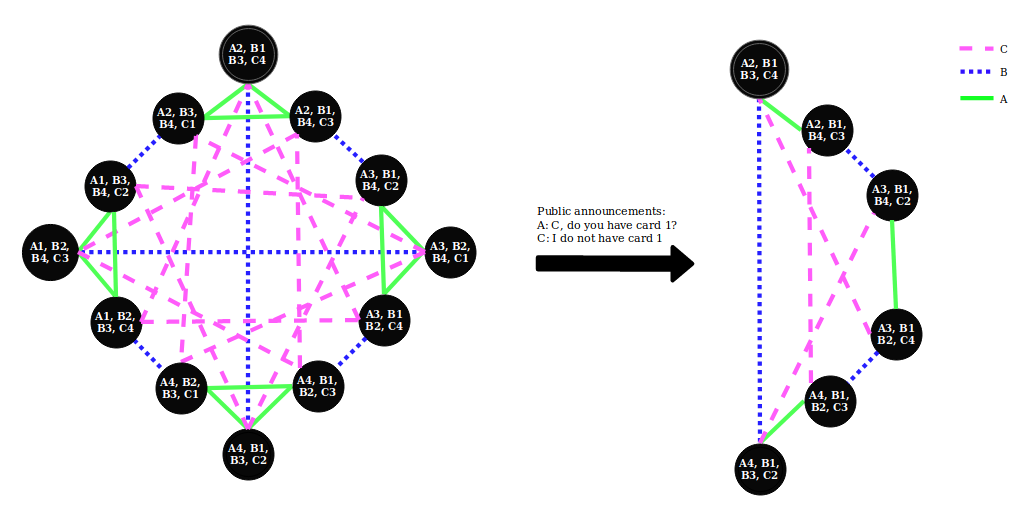
To make the relation with Kripke models more specific, we show in Figure 3 a Kripke model with the corresponding data structure that we use in Figure 4. In this example we have three players and one group of cards. Player B starts with two cards and player A and C start with one card. Player A then asks player C for card 1 after which player C announces she does not have this card. The data structure is only shown for player A, we have similar data structures for player B and C.

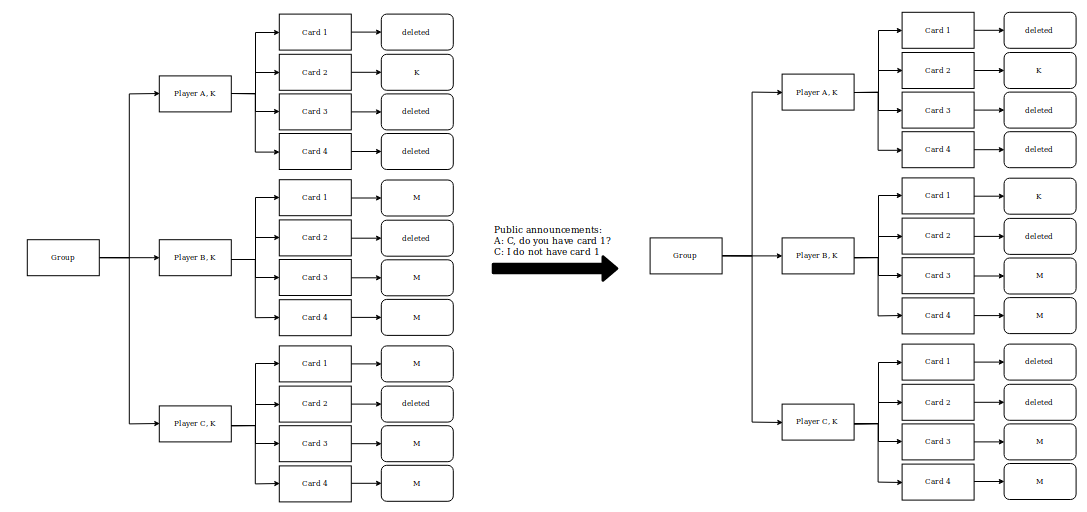
The model described so far can only store first-order logic. However, in a game of kwartet one also uses the knowledge of the other players. To store second-order, an extra layer, the observer, is added between group and player. If the observer is the player himself, then we have in that branch the model as it was before. However, if the observer is one of the opponents, a player stores what he knows about the opponents' knowledge. We could not think of kwartet strategies using third or even higher order logic. If you out-think us, note that higher order logic can be implemented similar to second order logic.

Actions

There are 5 actions that influence the knowledge structure (model):

• (Private) Seeing own cards: By the basic step of looking at which cards an agent has in his hand, we can update the model by removing worlds where these cards are owned by other players. This step is private for each individual agent.


• (Announcement) Requesting a card: According to the rules, requesting a card can only be done when you have a card from the group. This is a public announcement, so for each agent we update the model, replacing M(requested_group) because we have K(requested_group) for that agent.


• (Announcement) Giving a card: Giving a card is one of the most important announcements. After this action we update the model for each agent. Every agent knows that the player that was asked for the card does not have it any more. Every agent also knows that the player that asked for the card, has it now. Furthermore, they know that the agent that was asked for the card might not have cards of the mentioned group any longer. So, unless a player knows with certainty that the player who was requested a card has other cards of that group, he will set the group state for that player to M(group).


• (Announcement) Not giving a card: We update the model of each agent by removing the world were the asked agent has this card from the model.


• (Announcement) Kwartet!: We update each agent model by removing the group entirely from the model.

Furthermore we have 1 action that does not change the model but uses second order logic:

• (Private) Assess model (advanced thinking, not applied for all agents): By individually looking at what other agents know, the agent tries a different strategy of asking cards in the model.